Interpolasi
Linear : Hampiran nilai yang berada dalam suatu selang
Interpolasi
Polinomial Lagrange
f(x)
= pn(x) = a0.l0(x)+a1.l1(x)+...+an.ln(x)
ai
= yi
li(x)
= ∏j≠i(x-xj)/(xi-xj)
Contoh : Dari fungsi y = f(x) diberikan tiga buah titik data (1,1.5709), (4,1.5727), (6,1.5751), Tentukan f(3,5)
dengan polinom Lagrange derajat 2
Interpolasi
Polinomial Newton
pn(x)=a0
+ a1(x-x0) + a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)
an
= f[x0,x1,...,xn] f adalah beda terbagi
untuk 2 titik, f
adalah
3 titik
n
titik
Contoh : lakukan interpolasi Newton orde 3 melalui
titik (1, 0), (4,
1.386294), (6, 1.791759), (5, 1.609438)
p3(x)=a0
+ a1(x-x0) + a2(x-x0)(x-x1)+a3(x-x0)(x-x1)(x-x2)
p3(x) = 0+ 0.465(x-1)-0.053(x-1)(x-4)+0.008(x-1)(x-4)(x-6)
Vandermonde
Matrix
Bentuk umum dari
polinomial yang menginterpolasi titik (x0,y0),(x1,y1),...,(xn,yn)
adalah
Pn(x)
= a0 + a1x + a2x2 +...+anxn
Jika dimasukkan titik-titiknya akan membentuk sistem
persamaan linear
Dalam notasi matriks menjadi
Matriks V dalam
SPL tersebut adalah matriks Vandermonde
Interpolasi
Invers
Digunakan untuk menghampiri invers suatu fungsi
Galat
Interpolasi
Galat interpolasi adalah selisih antara hampiran
fungsi dengan fungsi sebenarnya
Teorema
I
Jika p adalah polinomial berderajat tertinggi n
yang menginterpolasi f pada n+1 titik, yaitu x0,x1,...,xn∈[a,b] dan jika f(n+1) kontinu,maka ∀x∈[a,b]
Galat
rata-rata interpolasi
c pada teorema I dihampiri dengan c
= xt = (x0 + xn)/2
Lemma
Batas Atas
Definisikan xi = a + ihxi untuk i=0, 1, …, n,
maka untuk suatu x∈[a,b],
dengan h=(b-a)/n
adalah jarak antartitik
Teorema II
Misalkan f fungsi yang memenuhi f(n+1) kontinu pada [a,b] dan |f(n+1)(x)|≤
M.
Misalkan p adalah polinomial berderajat ≤ n yang menginterpolasi
f pada n+1 titik di [a,b]
termasuk titik akhirnya ,maka di [a,b]
dengan h=(b-a)/n adalah jarak antartitik.
Turunan Numerik
Digunakan ketika
mencari turunan fungsi yang tidak diketahui atau memiliki bentuk rumit
Hampiran Selisih Maju
Misalkan x = x0 + h, dengan ekspansi
deret Taylor diperoleh
Dan diperoleh
hampiran turunan
Dengan galat
sebesar O(h)
Hampiran Selisih Mundur
Misalkan x = x0 - h, dengan ekspansi
deret Taylor diperoleh
Dan diperoleh
hampiran turunan
Dengan galat
sebesar O(h)
Hampiran Selisih Pusat
Dengan mengurangkan
ekspansi deret Taylor hampiran selisih maju dan hampiran selisih mundur,
diperoleh hampiran turunan
Dengan galat
sebesar O(h2)
Ekstrapolasi Richardson
Metode untuk
mencari hampiran turunan orde lebih tinggi dengan hampiran orde lebih rendah,
dan menghasilkan hasil yang lebih akurat
Dengan D(h) adalah hampiran turunan, dan n adalah orde galat



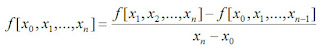









No comments:
Post a Comment